I love watching YouTube videos and as I’ve mentioned before, one of my favorite channels is Computerphile. They recently did a video talking about how to solve this sum:
23373 Mod 747
Their video was prompted by a video about Witness Numbers on the Numberphile channel, which I guess I now also need to subscribe to. This is the video description:
How do you compute a massive number raised to the power of another huge number, modulo something else? Dr Mike Pound explains the super-quick square & multiply algorithm.
Computerphile
I thought this posed an interesting question because that is obviously a huge number and is way bigger than most programming languages, including Xojo, can handle. However, taking the Mod means that the answer has to be between 0 and 746, so does the massive number actually need to be calculated at all?
It turns out the answer is no, as long as you know the algorithm, which is called Square & Multiply.
At a high level, this is the algorithm as explained in the video:
- Convert the exponent to binary.
- Each 0 requires a square
- Each 1 requires a square and then a multiply
- After each calculation, can do the modulo to keep the value small.
- The final calculation is the answer.
To test this, start with a smaller value. The video uses:
345 mod 7
The number 45 in binary is 101101. Since the very first digit is a 1, our starting value of this example is 3, the initial number itself.
- The next binary digit is 0, so that means a square. 3 * 3 = 9. 9 Mod 7 = 2.
- The next binary digit is 1, so that means a square and then a multiply.
- Squaring the 2 gives us 4 and the Mod 7 of that is also 4.
- We now use 4 and multiple it with the starting value of 3 to get 12. And 12 Mod 7 is 5.
As you can see, each time through we are only dealing with small numbers so they are easily calculated. And because the binary value of 45 only has 6 digits there will be at most 12 steps to the calculation, which is also much less than 45.
Continuing through the rest:
- Next binary digit is a 1, so square it: 5 * 5 = 25, Mod 7 = 4.
- and multiple it: 4 * 3 = 12, Mod 7 = 5.
- Next is a 0, so square it: 5 * 5 = 25, Mod 7 = 4.
- The last digit is a 1, so square it: 4 * 4 = 16, Mod 7 = 2.
- And finally multiply it: 2 * 3 = 6. 6 Mod 7 = 6, which the final answer.
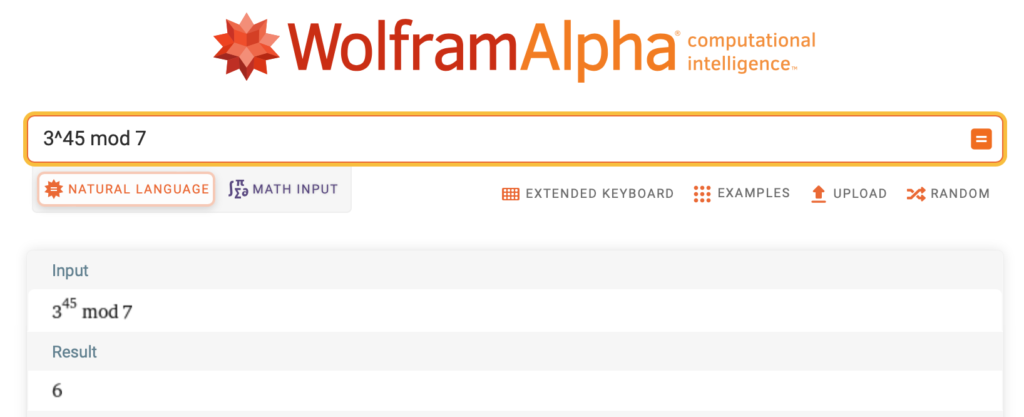
You can verify this using Wolfram Alpha:
Despite how it may seem, the above algorithm results in short method. Here’s what it looks like in Xojo:
Public Function SquareAndMultiply(value As Integer, exponent As Integer, modulus As Integer) As Integer
// Square and Multipe Algorithm
Var b As String = exponent.ToBinary
Var binaryValue() As String = b.Split("")
Var lastModulus As Integer = 1
Var newExp As Integer
newExp = Integer.FromBinary(binaryValue(0))
If binaryValue(0) = "1" Then
lastModulus = value
End If
For i As Integer = 1 To binaryValue.LastIndex
Var bit As String = binaryValue(i)
lastModulus = (lastModulus * lastModulus) Mod modulus
If bit = "1" Then // Multiply as well
lastModulus = (lastModulus * value) Mod modulus
End If
Next
Return lastModulus
End Function
I pretty much tried to implement the exact algorithm described in the video. The Wikipedia page on this topic seems to have other, perhaps more efficient, implementations.
You would call the Xojo method like this to solve the original problem shown a the top of this post:
Var answer As Integer = SquareAndMultiply(23, 373, 747)
You can download this Xojo project to try it out:
By the way, the answer to 23373 Mod 747 is 131.
Paul learned to program in BASIC at age 13 and has programmed in more languages than he remembers, with Xojo being an obvious favorite. When not working on Xojo, you can find him talking about retrocomputing at Goto 10 and on Mastodon @lefebvre@hachyderm.io.
